VECTOR
Vector es un término que deriva de un vocablo latino y que significa “que conduce”. Un vector es un agente que transporte algo de un lugar a otro. Su significado, de todas formas, varía de acuerdo al contexto.
Un vector puede utilizarse para representar una magnitud física, quedando definido por un módulo y una dirección u orientación. Su expresión geométrica consiste en segmentos de recta dirigidos hacia un cierto lado, asemejándose a una flecha. La velocidad y la fuerza son dos ejemplos de magnitudes vectoriales.
Dentro de este ámbito científico, y también de las Matemáticas, se hace necesario dejar patente que existe una gran variedad de vectores. De tal manera, que podemos hablar de fijos, paralelos, deslizantes, opuestos, concurrentes, libres o colineales, entre otros muchos más.
De la misma forma hay que subrayar que se pueden llevar a cabo un importante número de operaciones con dichos elementos. Entre las más frecuentes se encuentra la suma, el producto por un escalar, la obtención de una derivada ordinaria, las descomposiciones, el ángulo entre dos vectores o la derivada de tipo variante.
MAGNITUD
En Física, se llaman magnitudes a aquellas propiedades que pueden medirse y expresar su resultado mediante un número y una unidad. Son magnitudes las longitud, la masa, el volumen, la cantidad de sustancia, el voltaje, etc.
Las siguientes magnitudes se denominan magnitudes físicas fundamentales. Si a estas magnitudes se les añaden dos magnitudes complementarias: el ángulo sólido y el ángulo plano, a partir de ellas pueden expresarse TODAS las demás magnitudes físicas.
Las siguientes magnitudes se denominan magnitudes físicas fundamentales. Si a estas magnitudes se les añaden dos magnitudes complementarias: el ángulo sólido y el ángulo plano, a partir de ellas pueden expresarse TODAS las demás magnitudes físicas.
Una medición es el resultado de la acción de medir. Este verbo, con origen en el término latino metiri, se refiere a la comparación que se establece entre una cierta cantidad y su correspondiente unidad para determinar cuántas veces dicha unidad se encuentra contenida en la cantidad en cuestión.
Por ejemplo: “De acuerdo a la última medición, el pino que se encuentra junto al lago ya mide más de treinta metros”, “Antes de comprar el sillón, tenemos que realizar la medición del espacio disponible”, “La final del torneo fue seguida por TV por más de veinte millones de espectadores, según una medición de los organizadores”.
* CARACTERÍSTICAS DE UN VECTOR
Los vectores se representan por medio de flechas. El sentido del vector está dado por medio del indicador de la flecha o punta de flecha; la magnitud del vector está dado por el tamaño del vector y la dirección por la inclinación que tenga la flecha.
Generalmente el marco de referencia utilizado es el plano cartesiano, con el eje x positivo dirigido hacia la derecha y el eje y positivo dirigido hacia arriba.
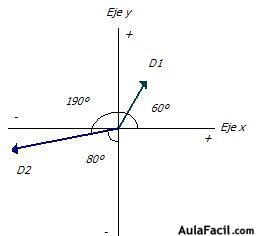
Ejemplo. Considere los vectores D1 (verde) y D2 (azul) representados en la figura. El vector D2 tiene mayor magnitud que el vector D1 (observe el tamaño).
Según el marco de referencia propuesto, ambos tienen sentidos opuestos y la dirección para D1 es 60º y para D2 es de 80º desde el eje negativo y (es decir, 190º).
Generalmente los vectores se representan con una letra (comúnmente la letra inicial de la propiedad que denota la cantidad) y encima de esa letra una flecha hacia la derecha. Por ejemplo:
Vector velocidad: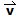 
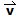
La magnitud de un vector se representa por medio de barras verticales:
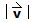Magnitud del vector velocidad.
La dirección del vector está dada por un ángulo θ con respecto al marco de referencia. Generalmente, éste ángulo se mide a partir del eje x positivo.
El sentido del vector está dado por el signo que lo antepone. Por ejemplo, si el vector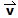 
está dirigido hacia el norte, entonces el vector -
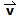está dirigido hacia el sur.
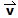está dirigido hacia el norte, entonces el vector - 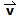está dirigido hacia el sur.
Las operaciones con vectores suelen ser más complejas debido a la introducción de las nuevas propiedades (dirección y sentido).
En las siguientes lecciones, se muestran algunos métodos para poder realizar sumas y restas de vectores.
*MAGNITUD ESCALAR Y MAGNITUD VECTORIAL.
Las magnitudes escalares tienen únicamente como variable a un número que representa una determinada cantidad. Por ejemplo la masa de un cuerpo, que se mide en Kilogramos.
Magnitudes vectoriales
En muchos casos las magnitudes escalares no dan información completa sobre una propiedad física. Por ejemplo una fuerza de determinado valor puede estar aplicada sobre un cuerpo en diferentes sentidos y direcciones. Tenemos entonces las magnitudes vectoriales que, como su nombre lo indica, se representan mediante vectores, es decir que además de un módulo (o valor absoluto) tienen una dirección y un sentido. Ejemplos de magnitudes vectoriales son la velocidad y la fuerza.
Según el modelo físico con el que estemos trabajando utilizamos vectores con diferente número de componentes. Los más comunes son los de una, dos y tres coordenadas que permiten indicar puntos en la recta, en el plano y en el espacio respectivamente.
En el apartado de matemática puedes consultar las operaciones con vectores más utilizadas (suma, resta, producto escalar, producto vectorial, etc).
Según el modelo físico con el que estemos trabajando utilizamos vectores con diferente número de componentes. Los más comunes son los de una, dos y tres coordenadas que permiten indicar puntos en la recta, en el plano y en el espacio respectivamente.
En el apartado de matemática puedes consultar las operaciones con vectores más utilizadas (suma, resta, producto escalar, producto vectorial, etc).
*SISTEMA DE VECTORES
Las magnitudes escalares tienen únicamente como variable a un número que representa una determinada cantidad. Por ejemplo la masa de un cuerpo, que se mide en Kilogramos.
Magnitudes vectoriales
En muchos casos las magnitudes escalares no dan información completa sobre una propiedad física. Por ejemplo una fuerza de determinado valor puede estar aplicada sobre un cuerpo en diferentes sentidos y direcciones. Tenemos entonces las magnitudes vectoriales que, como su nombre lo indica, se representan mediante vectores, es decir que además de un módulo (o valor absoluto) tienen una dirección y un sentido. Ejemplos de magnitudes vectoriales son la velocidad y la fuerza.
Según el modelo físico con el que estemos trabajando utilizamos vectores con diferente número de componentes. Los más comunes son los de una, dos y tres coordenadas que permiten indicar puntos en la recta, en el plano y en el espacio respectivamente.
En el apartado de matemática puedes consultar las operaciones con vectores más utilizadas (suma, resta, producto escalar, producto vectorial, etc).
Según el modelo físico con el que estemos trabajando utilizamos vectores con diferente número de componentes. Los más comunes son los de una, dos y tres coordenadas que permiten indicar puntos en la recta, en el plano y en el espacio respectivamente.
En el apartado de matemática puedes consultar las operaciones con vectores más utilizadas (suma, resta, producto escalar, producto vectorial, etc).
*SISTEMA DE VECTORES
Se tiene un sistema de vectores colineales cuando dos o mas vectores se encuentran en la misma dirección, aunque tenga diferente sentido.
*REFERENCIAS
http://definicion.de/vector/
http://newton.cnice.mec.es/materiales_didacticos/magnitudes/magnitudes.html
http://definicion.de/medicion/
http://www.aulafacil.com/cursos/l10313/ciencia/fisica/fisica-general-ii/caracteristicas-de-los-vectores
http://www.fisicapractica.com/magnitudes.php
http://cibertareas.info/vectores-colineales-sistema-de-vectores.html
ELABORADO POR:
Priscyla Alejandra Zamora Nolasco.
Diana Edith Vargas Morales
Eliasim Gonzalez Alva.
No hay comentarios:
Publicar un comentario